承上一篇,若不使用Eval Polar to Rect.vi元件時,要如何把函數拆解成X軸和Y軸的2個陣列資料?
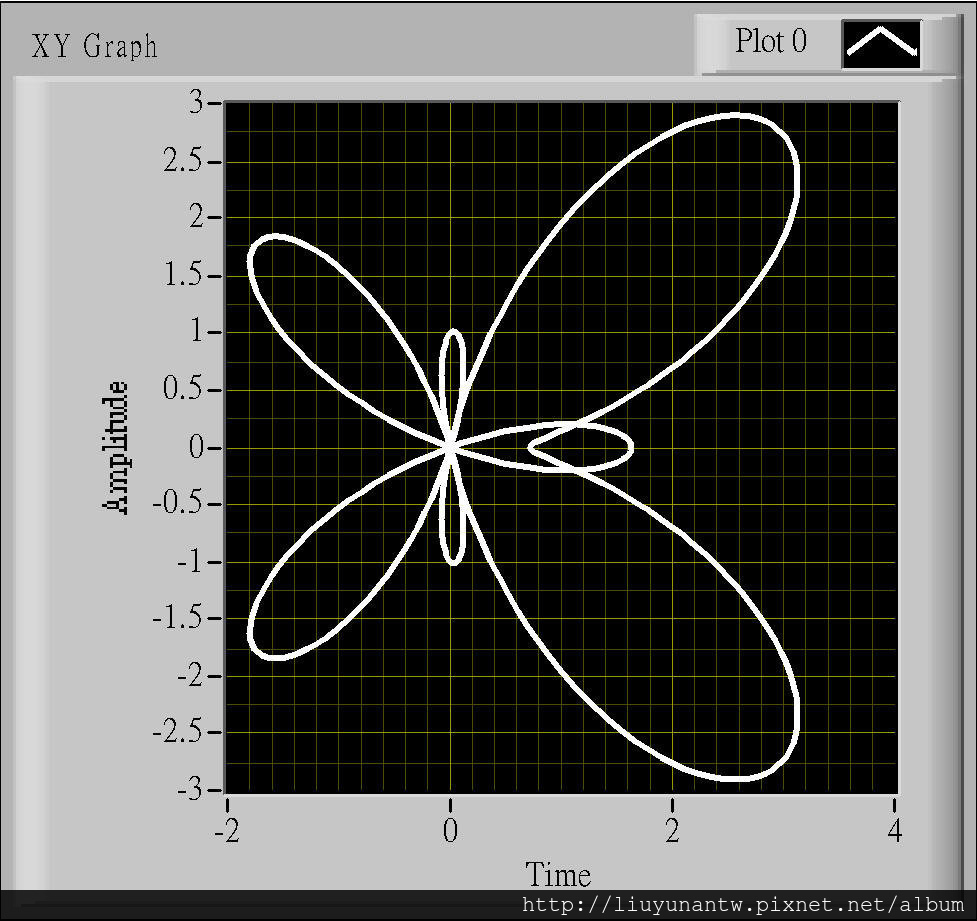
同樣用上一篇蝴蝶圖的函數來說明如何拆解:
原函數若要完全拆解會弄的很複雜,這裡只取單一線條的基本圖形函數來拆解
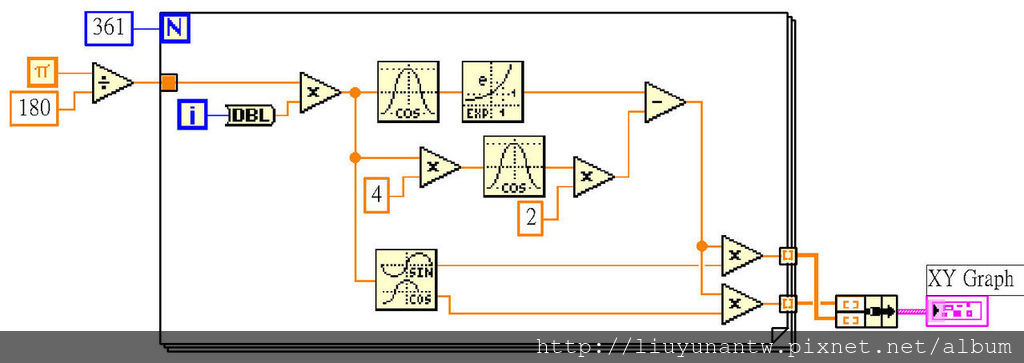
基本函數:exp(cos(t))-2*cos(4*t)
拆解的要領是原函數分別乘上sin(t)和cos(t)即可
X軸函數:(exp(cos(t))-2*cos(4*t))*cos(t)
Y軸函數:(exp(cos(t))-2*cos(4*t))*sin(t)
t這個變數是什麼呢?其實就是θ也就是徑度和角度的轉換,也就是pi/180*i
其他類似的函數一概適用這種拆解法,後續的文章會提到其他函數
以拆解出的函數來完成程式
執行後可看到是單一線條橫向的蝴蝶,要放正同樣就把X軸和Y軸對調
這種拆解法用在有不只t一項變數的函數時
文章標籤
全站熱搜


 留言列表
留言列表

